2022. 8. 18. 17:05ㆍ알고리즘/programmers
안녕하세요.
또 어려운 문제가 왔습니다... 이번엔 연결리스트에 관한 문제입니다.
특히 삭제나 삽입에 대해서 알아볼 수 있는 좋은 기회입니당..
자 같이 한 번 볼까요?
(그리고 이 문제 js로 구현하신 블로거 분들이 다 한 코드를 보고 복사하신건지 다 코드가 똑같더라구요..)
문제 요약
업무용 소프트웨어를 개발하는 니니즈웍스의 인턴인 앙몬드는 명령어 기반으로 표의 행을 선택, 삭제, 복구하는 프로그램을 작성하는 과제를 맡았습니다. 세부 요구 사항은 다음과 같습니다
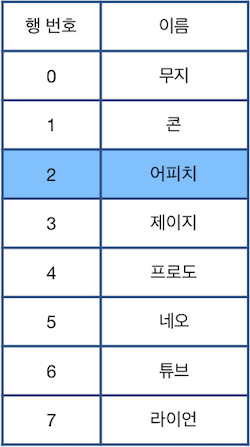
위 그림에서 파란색으로 칠해진 칸은 현재 선택된 행을 나타냅니다. 단, 한 번에 한 행만 선택할 수 있으며, 표의 범위(0행 ~ 마지막 행)를 벗어날 수 없습니다. 이때, 다음과 같은 명령어를 이용하여 표를 편집합니다.
- "U X": 현재 선택된 행에서 X칸 위에 있는 행을 선택합니다.
- "D X": 현재 선택된 행에서 X칸 아래에 있는 행을 선택합니다.
- "C" : 현재 선택된 행을 삭제한 후, 바로 아래 행을 선택합니다. 단, 삭제된 행이 가장 마지막 행인 경우 바로 윗 행을 선택합니다.
- "Z" : 가장 최근에 삭제된 행을 원래대로 복구합니다. 단, 현재 선택된 행은 바뀌지 않습니다.
제한 사항
- 5 ≤ n ≤ 1,000,000
- 0 ≤ k < n
- 1 ≤ cmd의 원소 개수 ≤ 200,000
- cmd의 각 원소는 "U X", "D X", "C", "Z" 중 하나입니다.
- X는 1 이상 300,000 이하인 자연수이며 0으로 시작하지 않습니다.
- X가 나타내는 자연수에 ',' 는 주어지지 않습니다. 예를 들어 123,456의 경우 123456으로 주어집니다.
- cmd에 등장하는 모든 X들의 값을 합친 결과가 1,000,000 이하인 경우만 입력으로 주어집니다.
- 표의 모든 행을 제거하여, 행이 하나도 남지 않는 경우는 입력으로 주어지지 않습니다.
- 본문에서 각 행이 제거되고 복구되는 과정을 보다 자연스럽게 보이기 위해 "이름" 열을 사용하였으나, "이름"열의 내용이 실제 문제를 푸는 과정에 필요하지는 않습니다. "이름"열에는 서로 다른 이름들이 중복없이 채워져 있다고 가정하고 문제를 해결해 주세요.
- 표의 범위를 벗어나는 이동은 입력으로 주어지지 않습니다.
- 원래대로 복구할 행이 없을 때(즉, 삭제된 행이 없을 때) "Z"가 명령어로 주어지는 경우는 없습니다.
- 정답은 표의 0행부터 n - 1행까지에 해당되는 O, X를 순서대로 이어붙인 문자열 형태로 return 해주세요.
테스트케이스
| n | k | cmd | result |
| 8 | 2 | ["D 2","C","U 3","C","D 4","C","U 2","Z","Z"] | "OOOOXOOO" |
| 8 | 2 | ["D 2","C","U 3","C","D 4","C","U 2","Z","Z","U 1","C"] | "OOXOXOOO" |
접근 방법
연결리스트를 구현해본 적이 있다면 생각보다 직관적으로 보입니다.
[JS] 연결리스트에 대해서
안녕하세요. 카카오 2021 인턴 표 편집을 하던도중 이건 그냥 봐도 연결리스트를 쓰라는 것 같더라구용. 자바스크립트에서 한 번도 연결리스트를 써본 적이 없었는데 구현 코드를 보니 상당합니
dev-russel.tistory.com
이전에 쓴 포스트에서처럼 stack 형태의 구조에서 중간에서 삭제, 삽입이 이뤄지기 때문입니다.
다만, 삽입/삭제를 어떻게 효율적으로 할 수 있는가?는 이번 문제를 통해서 명확히 아실 수 있을 겁니다.
해당 조작을 위해서 탐색이 선행되지 않게끔 하는 방법이 있거든요.
연결리스트에서 탐색은 O(n), 삽입/삭제는 O(1)의 시간 복잡도를 가집니다.
일반적인 배열(스택)에서는 탐색이 O(n), 삽입/삭제 역시 O(n)의 시간복잡도를 가집니다.
결론적으로 우리가 효율적으로 연결리스트를 이용하기 위해서는,
삽입/삭제 작업 시 전체 연결리스트를 탐색하지 않는 방향으로 해야한다는 점이 중요하겠습니다.
일단 처음에 제가 짰던 탐색을 쓰는 비효율적인 연결리스트(단방향 연결리스트) 코드를 먼저 볼까요?
1. 오답 코드 - 효율성 테스트 통과 X
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class LinkedList {
constructor() {
this.head = null;
this.tail = null;
this.size = 0;
}
find(value) {
let currNode = this.head;
while (currNode.value < value) {
if (currNode.next) {
if (currNode.next.value < value) currNode = currNode.next;
else return currNode;
} else break;
}
return currNode;
}
append(value) {
const node = new Node(value);
if (!this.head) {
this.head = node;
this.tail = node;
} else {
this.tail.next = node;
this.tail = node;
}
this.size++;
}
insert(index, value) {
const newNode = new Node(value);
let node = this.head;
let currIdx = 1;
while (currIdx < index) {
node = node.next;
currIdx++;
}
newNode.next = node.next;
node.next = newNode;
this.size++;
}
remove(current) {
let prevNode = this.head;
if (current === 0) {
this.head = prevNode.next;
return prevNode.value;
}
let currIdx = 1;
while (currIdx !== current) {
prevNode = prevNode.next;
currIdx++;
}
const val = prevNode.next.value;
if (prevNode.next) {
prevNode.next = prevNode.next.next;
}
this.size--;
return val;
}
display() {
let currNode = this.head;
const result = [];
while (currNode) {
result.push(currNode.value);
currNode = currNode.next;
}
return result;
}
}
function bsearch(target, arr) {
let [pl, pr] = [0, arr.length - 1];
let mid = Math.floor((pl + pr) / 2);
while (pl <= pr) {
if (arr[mid] === target) return true;
if (arr[mid] > target) {
pr = mid - 1;
} else {
pl = mid + 1;
}
mid = Math.floor((pl + pr) / 2);
}
return false;
}
function solution(n, k, cmd) {
let current = k;
const linkedList = new LinkedList();
// const table = Array.from({length: n}, (_, i) => i);
const memento = [];
for (let i = 0; i < n; i++) {
linkedList.append(i);
}
for (const command of cmd) {
if (command === "C") {
memento.push([current, linkedList.remove(current)]);
if (current === linkedList.size) current--;
} else if (command === "Z") {
const [index, value] = memento.pop();
linkedList.insert(index, value);
if (index <= current) current++;
} else {
const [dir, move] = command.split(" ");
if (dir === "U") current -= Number(move);
else current += Number(move);
}
}
const result = linkedList.display();
let answer = "";
for (let i = 0; i < n; i++) {
if (result.includes(i)) answer += "O";
else answer += "X";
}
return answer;
// return table.reduce((acc, val, i) => acc += bsearch(val, result) ? "O" : "X", "");
}실행 결과
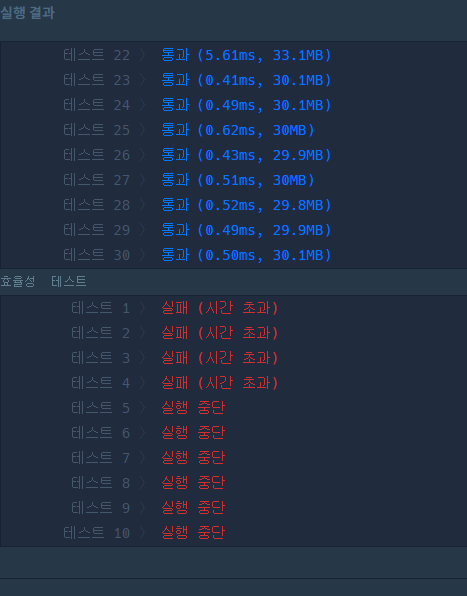
왜 통과하지 못했나요? - insert/remove에 대해서
insert(index, value) {
const newNode = new Node(value);
let node = this.head;
let currIdx = 1;
while (currIdx < index) {
node = node.next;
currIdx++;
}
newNode.next = node.next;
node.next = newNode;
this.size++;
}
remove(current) {
let prevNode = this.head;
if (current === 0) {
this.head = prevNode.next;
return prevNode.value;
}
let currIdx = 1;
while (currIdx !== current) {
prevNode = prevNode.next;
currIdx++;
}
여기 코드를 보시면 바깥의 current라는 index를 이용한 반복문을 통해서 head부터 탐색을 수행하도록 설계되어 있습니다.
단방향 연결리스트로 구현을 하면 이렇게 할 수 밖에 없는게,
remove의 이전 노드(편의상 prev라고 하겠습니다.)를 알 방법이 없기 때문입니다.
조작할 때, prev.next = node; 로 변경을 해줘야하기 때문이죠.
그런데 여기에서 문제가 되는게, 연결리스트를 순회하면 사실상 2중 loop가 되기 때문입니다.
연결리스트의 요소는 n을 따르기 때문에 최대 1,000,000 개가 형성될 수 있습니다.
cmd 루프 중에 몇 번이나 삭제/복구를 해주는데, 그 때마다 백 만 번을 순회하고 있으니 당연히 통과할 수 가 없는거죠.
결론적으로 이 문제는 효율성 테스트를 통과하기 위해서라도 양방향 리스트가 강제됩니다.
그렇다면 insert나 remove도 약간의 변화가 필요하겠네요.
자 그럼 진짜 답을 볼까요?
2. 정답코드 - 양방향 리스트를 이용한 풀이
class Node {
constructor(value) {
this.value = value;
this.next = null;
this.prev = null;
}
}
class LinkedList {
constructor() {
this.head = null;
this.size = 0;
}
move(dir, move, current) {
let currNode = current;
let unit = 0;
if (dir === "U") {
while (unit < move) {
if (currNode.prev) {
currNode = currNode.prev;
} else break;
unit++;
}
} else {
while (unit < move) {
if (currNode.next) {
currNode = currNode.next;
} else break;
unit++;
}
}
return currNode;
}
append(value, prev) {
const node = new Node(value);
if (prev) {
prev.next = node;
node.prev = prev;
}
if (!this.head) {
this.head = node;
}
this.size++;
return node;
}
recover(node) {
const [prev, next] = [node.prev, node.next];
if (prev) prev.next = node;
else this.head = node;
if (next) next.prev = node;
this.size++;
}
remove(node) {
const [prev, next] = [node.prev, node.next];
if (prev) prev.next = next;
else this.head = next;
if (next) next.prev = prev;
this.size--;
return next ? next : prev;
}
display() {
let currNode = this.head;
const result = [];
while (currNode) {
result.push(currNode.value);
currNode = currNode.next;
}
return result;
}
}
function bsearch(target, arr) {
let [pl, pr] = [0, arr.length - 1];
let mid = Math.floor((pl + pr) / 2);
while (pl <= pr) {
if (arr[mid] === target) return true;
if (arr[mid] > target) {
pr = mid - 1;
} else {
pl = mid + 1;
}
mid = Math.floor((pl + pr) / 2);
}
return false;
}
function solution(n, k, cmd) {
const linkedList = new LinkedList();
const table = Array.from({length: n}, (_, i) => i);
const memento = [];
let prev = null;
let current = null;
table.forEach((v, i) => {
prev = linkedList.append(i, prev);
if (i === k) current = prev;
});
for (const command of cmd) {
if (command === "C") {
memento.push(current);
current = linkedList.remove(current);
} else if (command === "Z") {
const node = memento.pop();
linkedList.recover(node);
} else {
const [dir, move] = command.split(" ");
current = linkedList.move(dir, Number(move), current);
}
}
const result = linkedList.display().sort((a, b) => a - b);
return table.reduce((acc, val, i) => acc += bsearch(val, result) ? "O" : "X", "");
}실행 결과
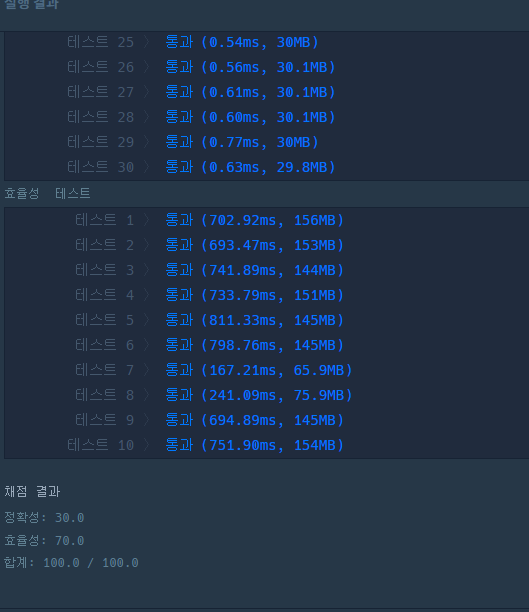
오히려 solution 안의 코드는 직관적인데 의외로 append 구현에 좀 애먹었습니다.
다른 분들 코드를 스리슬쩍 참고했었는데, 단방향 리스트와 다르게 tail로 조작하는게 아니더라구요. 이전 노드를 외부에서 저장한 다음, 직접 prev 속성에 그 노드를 넣어주는 개념이었습니다.
또 중요한 부분이 하나 있는데요. 바로 head 설정에 관한 부분입니다.
팁. head를 잘 설정해야합니다.
recover(node) {
const [prev, next] = [node.prev, node.next];
if (prev) prev.next = node;
// prev가 null이라면 head를 복구한다는 뜻입니다.
else this.head = node;
if (next) next.prev = node;
this.size++;
}
remove(node) {
const [prev, next] = [node.prev, node.next];
if (prev) prev.next = next;
// prev가 null이라면 head를 지운다는 뜻입니다.
else this.head = next;
if (next) next.prev = prev;
this.size--;
return next ? next : prev;
}
head를 지우는 경우, 연결리스트를 stack으로 변환시켜주는 display()함수가 항상 head부터 시작하기 때문에,
아예 루프를 타지 않는 버그를 발견했습니다.
따라서, 삭제/복구 시 prev가 null인지를 꼭 따져서(이전 노드가 없으니 head라는 뜻입니다.)
적절히 head를 조작해줘야합니다.
진짜 어려웠습니다. 꼬박 하루가 걸렸네요.
그런데 의미 있었습니다. 연결리스트 사용법을 알게 해준 고마운 문제였습니다.
그럼 이만!
'알고리즘 > programmers' 카테고리의 다른 글
| [JS] 등산코스 정하기 - 다익스트라 알고리즘에 대해서 (0) | 2022.08.24 |
|---|---|
| [JS] 전력망을 둘로 나누기 - bfs에서 약간만 응용해보자! (0) | 2022.08.20 |
| [JS] 셔틀버스 - 시간을 비교할땐 항상 조심하자! (0) | 2022.08.16 |
| [JS] 자물쇠와 열쇠 - 디버깅 지옥 멈춰! true/false 멈춰! (0) | 2022.08.10 |
| [JS] 다단계 칫솔 판매 (0) | 2022.08.08 |