2022. 9. 18. 17:00ㆍ알고리즘
힙과 트리는 꽤 비슷한 자료구조 같지만 명확한 차이가 있습니다.
트리를 다뤄야 하는 문제에서 힙을 다뤘을 때 생길 수 있는 문제점에 대해서 기록해보려고 합니다.
1. 힙(Heap)
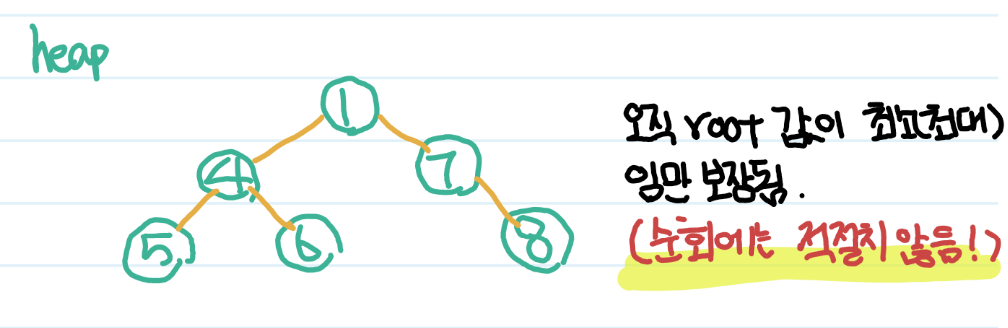
항상 이진 트리 구조를 구현할 때 관성적으로 heap을 사용하곤 했는데요.
heap 구조는 탐색에 적절하진 않습니다.
parent node에 대해서 child node가 항상 차 있지 않는 경우가 있기 때문입니다.
주로 heap은 우선 순위 큐의 구현을 위해 사용합니다.
[JS] 힙/우선 순위 큐 새로 짜봤습니다.
Javascript에서 힙이 필요하면 매번 구현을 해줘야하는 정말.. 험난한 여정이 있는데요. 저번에 제가 대략적으로 공유한 코드가 모든 상황에서 쓰이기 힘들더라구요. 특히 pop에서 최상단 노드부터
dev-russel.tistory.com
class Heap {
contructor(){
this.heap = [null]; // 주로 배열로 구현. [null, 1, 3, 4, 7, 8]
}
//...
}
자료 구조를 일반 stack으로 관리하기 때문에 부모노드에서 자식 노드에 있는 값을 판단하기가 어렵습니다.
2. 트리(Tree)

일반적으로 트리는 순회에 적합한 자료구조입니다.
현재 노드의 값 뿐만 아니라 left, right에 대한 정보를 함께 알 수 있기 때문에
부모 노드에서 자식 노드로 접근할 때 접근 편의성이 훨씬 좋습니다.
Tree.js (with LinkedList)
class Node {
contructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class Tree {
constructor(node) {
this.root = node;
}
push(node) {
let currNode = this.root;
while (currNode) {
if (node.val > currNode.val) {
if (currNode.right) currNode = currNode.right;
else {currNode.right = node; break;}
} else {
if (currNode.left) currNode = currNode.left;
else {currNode.left = node; break;}
}
}
}
preorder(currnode, order) {
if (currnode) {
order.push(currnode.val);
this.preorder(currnode.left, order);
this.preorder(currnode.right, order);
}
}
postorder(currnode, order) {
if (currnode) {
this.postorder(currnode.left, order);
this.postorder(currnode.right, order);
order.push(currnode.val);
}
}
}
그냥 array로 구현해도 되지만, 연결리스트로 구현해야 left, right로의 접근이 용이해집니다.
전위순회와 후위 순회를 보면 인자로 currnode와 order를 넣게 되는데
currnode는 tree의 root를 넣어주면 되고, order는 계속 collecting 할 수 있는 배열을 넣어주면 됩니다.
예를 들면 이런 식으로 해주시면 되어요.
const tree = new Tree(7);
tree.push(new Node(6));
tree.push(new Node(5));
tree.push(new Node(4));
tree.push(new Node(3));
const [preorder, postorder] = [[], []];
tree.preorder(tree.root, preorder);
tree.postorder(tree.root, postorder);
캡슐화를 위반하는 것 같아서 너무 불편하다 싶으시면
Tree 클래스 안에 getter를 하나 만드시는게 여러분을 편하게 만들 수 있습니다.
tree는 잘 안쓰이지만 언젠가 한 번은 꼭 쓰일 때가 있더라구요.
그럼 이만!
'알고리즘' 카테고리의 다른 글
| [JS] 파괴되지 않은 건물: (new) 누적합 (1) | 2022.09.20 |
|---|---|
| [JS] 플로이드-워셜 알고리즘: 다익스트라 같은데 뭔가 안될때 (0) | 2022.09.01 |
| 배열을 90도 회전시키는 방법 (0) | 2022.08.09 |