2022. 9. 20. 00:21ㆍ알고리즘
새로운 알고리즘입니다!
배열의 일정 구간을 일괄적으로 N만큼 조작하고 싶을 때 사용할 수 있습니다.먼저 문제를 보죠!
문제 요약
N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.
적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.
예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.

첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.

두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.

세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.

마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)
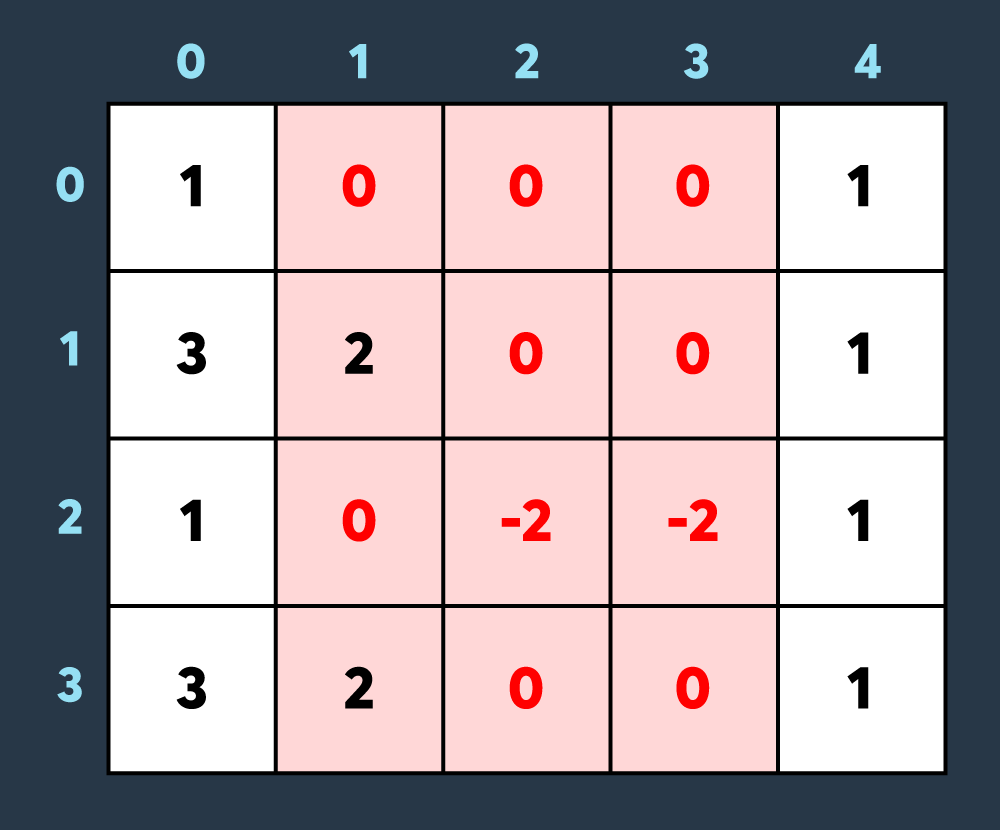
최종적으로 총 10개의 건물이 파괴되지 않았습니다.
건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.
제한사항
- 1 ≤ board의 행의 길이 (= N) ≤ 1,000
- 1 ≤ board의 열의 길이 (= M) ≤ 1,000
- 1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
- 1 ≤ skill의 행의 길이 ≤ 250,000
- skill의 열의 길이 = 6
- skill의 각 행은 [type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.
- type은 1 혹은 2입니다.
- type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
- type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
- (r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
- 0 ≤ r1 ≤ r2 < board의 행의 길이
- 0 ≤ c1 ≤ c2 < board의 열의 길이
- 1 ≤ degree ≤ 500
- type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
- type이 2이면 degree만큼 건물의 내구도를 높입니다.
- type은 1 혹은 2입니다.
- 건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.
정확성 테스트 케이스 제한 사항
- 1 ≤ board의 행의 길이 (= N) ≤ 100
- 1 ≤ board의 열의 길이 (= M) ≤ 100
- 1 ≤ board의 원소 (각 건물의 내구도) ≤ 100
- 1 ≤ skill의 행의 길이 ≤ 100
- 1 ≤ degree ≤ 100
효율성 테스트 케이스 제한 사항
- 주어진 조건 외 추가 제한사항 없습니다.
테스트케이스
| board | skill | result |
| [[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5],[5,5,5,5,5]] | [[1,0,0,3,4,4],[1,2,0,2,3,2],[2,1,0,3,1,2],[1,0,1,3,3,1]] | 10 |
| [[1,2,3],[4,5,6],[7,8,9]] | [[1,1,1,2,2,4],[1,0,0,1,1,2],[2,2,0,2,0,100]] | 6 |
접근 방법
그냥 딱 보면 되게 쉬워보입니다.
그냥 3중 loop 중첩해서 푸는 방법이 있죠.
다만, 이 방법은 효율성 테스트에서 걸리게 설계 되어 있습니다.
정답 코드?
function solution(board, skill) {
for (const [type, r1, c1, r2, c2, degree] of skill) {
for (let i = r1; i <= r2; i++) {
for (let j = c1; j <= c2; j++) {
board[i][j] += type === 1 ? (-degree) : (degree);
}
}
}
return board.flat(1).filter(v => v > 0).length;
}실행 결과
누적합 개념을 적용해야 하는데 생전 처음 봅니다.
친절한 카카오 해설에 너무나도 자세하게 적혀있네요. 이런 생각은 해보지도 못했거든요..
(정답 코드 아래 팁 부분에서 누적합을 제 나름대로 정리해봤습니다!)
2022 카카오 신입 공채 1차 온라인 코딩테스트 for Tech developers 문제해설
지난 2021년 9월 11일 토요일 오후 2시부터 7시까지 5시간 동안 2022 KAKAO BLIND RECRUITMENT 1차 코딩 테스트가 진행되었습니다. 테스트에는 총 7개의 문제가 출제되었으며, 개발 언어는 C++, Java, JavaScript, K
tech.kakao.com
진짜 정답코드 with 누적합
function solution(board, skill) {
const partialSums = Array.from({ length: board.length + 1 }, () => Array.from({ length: board[0].length + 1 }, () => 0));
let answer = 0;
for (const [type, r1, c1, r2, c2, degree] of skill) {
partialSums[r1][c1] += type === 1 ? (-degree) : degree;
partialSums[r1][c2 + 1] += type === 1 ? degree : (-degree);
partialSums[r2 + 1][c1] += type === 1 ? degree : (-degree);
partialSums[r2 + 1][c2 + 1] += type === 1 ? (-degree): degree;
}
partialSums.forEach((rows) => {
let sum = 0;
for (let i = 0; i < rows.length; i++) {
sum += rows[i];
rows[i] = sum;
}
});
for (let i = 0; i < partialSums[0].length; i++) {
let sum = 0;
for (let j = 0; j < partialSums.length; j++) {
sum += partialSums[j][i];
partialSums[j][i] = sum;
}
}
for (let i = 0; i < board.length; i++) {
for (let j = 0; j < board[0].length; j++) {
board[i][j] += partialSums[i][j];
if (board[i][j] > 0) answer++;
}
}
return answer;
}실행결과

팁 1. 누적합
const arr = [5, 3, 2, 4, 9, 8];
// index 0 ~ 2까지 2을 더하고 싶다면?
const partialSums = [2, 0, 0, -2];
// 누산기 계산 => [2, 2, 2, 0];
// arr에 더해주기!
let sum = 0;
for (let i = 0; i < partialSums.length; i++) {
sum += partialSums[i];
partialSums[i] = sum;
}
for (let i = 0; i < arr.length; i++) {
arr[i] += partialSums[i];
}
// => [7, 5, 4, 6, 9, 8];
누적합은 배열의 특정 구간을 조작해야하는 행위가 여러번 일어날 때 유용합니다.
그냥 한 번만 수행하는 예시를 보면 그냥 index로 조작하는게 쉽지 않나..? 하는 생각이 드는데요.
이런 상황이 배열로 주어진다면 당연히 2중 loop 구성으로 해결합니다. 하지만 이 방법을 쓰면 중첩하지 않고도 해결할 수 있다는 장점이 있습니다.
팁 2. 2중 배열에서 누적합
// (0, 0)에서부터 (2, 2) 까지 3을 빼고 싶다면?
// 결론적으로 이런 모양이 나오면 되지 않을까..?
const target = [
[-3, -3, -3, 0],
[-3, -3, -3, 0],
[-3, -3, -3, 0],
[0, 0, 0, 0]
]
// 누적합 offset 배열 형태로 변환한다면?
const partialSums = [
[-3, 0, 0, 3],
[0, 0, 0, 0],
[0, 0, 0, 0],
[3, 0, 0, -3]
];
// 이 배열을 행기준으로 합하면?
[
[-3, -3, -3, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[3, 3, 3, 0]
]
//이 배열을 열 기준으로 합하면? => target 완성!
결론적으로 2차원 배열 상황에서 부분합 offset 배열을 이렇게 처리해주면 됩니다.
// r1, c1, r2, c2, degree라면?
partialSums[r1][c1] = degree;
partialSums[r1][c2 + 1] = -degree;
partialSums[r2 + 1][c1] = -degree;
partialSums[r2 + 1][c2 + 1] = degree;
우리는 type에 따라 degree앞에 -를 붙혀주면 되겠네요.
그 이후로는 partialSums를 행에 따라, 열에 따라 합쳐주는 과정입니다.
해당 방법으로 O(N * M * K) 였던 시간복잡도를 O(N * M + K)로 줄일 수 있었습니다.
[N: board의 행, M: board의 열, K: skill의 갯수]
진짜 뭔 별별 알고리즘이 다있네요.
그럼 이만!
'알고리즘' 카테고리의 다른 글
| [JS] 트리와 힙의 차이는 뭘까? (0) | 2022.09.18 |
|---|---|
| [JS] 플로이드-워셜 알고리즘: 다익스트라 같은데 뭔가 안될때 (0) | 2022.09.01 |
| 배열을 90도 회전시키는 방법 (0) | 2022.08.09 |