2022. 9. 17. 17:30ㆍ알고리즘/programmers
새로운 알고리즘이네요.그리디(Greedy) 알고리즘의 일종인 크루스칼(Kruskal) 알고리즘 입니다.
크루스칼 알고리즘
- 목적: 최소 신장 트리 구하기
- 주요 기능: Union - Find를 통한 최소 비용외의 간선 삭제

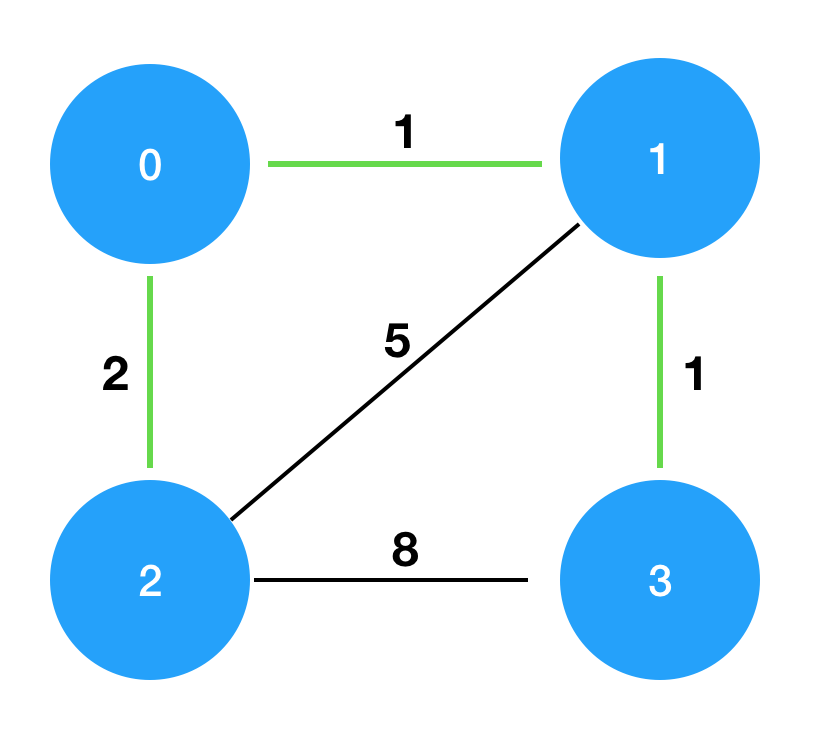
이런 노드들이 있다고 가정하면, 간선 [3 - 4]를 제외한 경로가 비용이 최소가 되는 경로입니다.
이런 경로를 구하는 방법은 다음과 같습니다.
1. 비용의 순서대로 정렬.
2. 해당 노드의 부모를 갱신.
3. 비용 계산으로 진행됩니다.

union - find 연산은 node의 부모가 다를때 각 노드의 부모를 갱신해주는 알고리즘입니다.
부모가 같다면 해당 간선으로 사이클이 발생할 수 있기 때문에 부모가 같은 경우는 제외하게 됩니다.
종종 union 연산 시 갱신하는 parent가 최상단의 root가 아닌 경우가 있습니다.
이런 경우를 위해서 find 연산으로 찾는 부모는 재귀함수를 통해 최상단 노드로 가줍시다.
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
테스트케이스
| n | cost | return |
| 4 | [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] | 4 |
접근 방법
전형적인 크루스칼 알고리즘에 관한 문제입니다.
union-find가 처음 구현할때는 꽤 생소해서 어려울 수 있으니 흐름을 잘 따라가보죠!
정답 코드
function solution(n, costs) {
costs.sort((a, b) => a[2] - b[2]);
const parent = Array.from({ length: n }, (_, i) => i);
let result = 0;
for (const [start, end, cost] of costs) {
if (!isSameParent(parent, start, end)) {
result += cost;
union(parent, start, end);
}
}
return result;
}
function union(parent, a, b) {
a = find(parent, a);
b = find(parent, b);
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
function isSameParent(parent, a, b) {
a = find(parent, a);
b = find(parent, b);
return a === b;
}
function find(parent, x) {
if (parent[x] === x) {
return x;
}
return parent[x] = find(parent, parent[x]);
}
팁 1. find 함수
function find(parent, x) {
if (parent[x] === x) {
return x;
}
return parent[x] = find(parent, parent[x]);
}
parent 배열의 index와 값은 자기 자신으로 초기화됩니다.
그렇기 때문에 가장 최상단 root 노드의 index와 value는 항상 같다고 보장됩니다.
find함수를 통해 재귀로 호출해줍시다. 이를 통해 최상단 노드의 index를 알 수 있습니다.
팁 2. union 함수
function union(parent, a, b) {
a = find(parent, a);
b = find(parent, b);
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
a와 b가 같은 부모노드가 아니기 때문에 한 간선으로 연결해주는 순간 부모노드를 같게 해주는
union 처리를 해줄 필요가 있습니다.
간선 정보의 대소 관계가 보장되어있지 않기 때문에 둘 중 작은 부모노드로 같이 union 시켜줍시다.
자주 다루기 힘든 크루스칼 알고리즘입니다.
불필요한 경로를 제거해야하는 경우에 이용해주면 유용합니다.
그럼 이만!
'알고리즘 > programmers' 카테고리의 다른 글
| [JS] 광고 삽입 - 누적합의 활용 2 (1) | 2022.09.22 |
|---|---|
| [JS] 길찾기 게임 - 하발자 특(나): 힙 씀, 상발자 특: 트리 씀 (0) | 2022.09.19 |
| [JS] 숫자 게임 - 비겼을 때 처리를 해주자! (0) | 2022.09.14 |
| [JS] 최고의 집합: 산술-기하 평균으로 접근해보자! (0) | 2022.09.12 |
| [JS] 성격 유형 검사하기: 난 해시맵이 좋아! (0) | 2022.09.08 |